データサイエンス学習の中でも最も面白い機械学習。
一言で機械学習といっても多くのアルゴリズムが存在します。解きたい課題によって適切なアルゴリズムを実装していくことが肝となりますが、そのためにはそれぞれのアルゴリズムの概要を理解している必要があります。
本記事では機械学習アルゴリズムの全体像および概要をご紹介します。
機械学習アルゴリズム全体像
個別のアルゴリズムを学ぶ前に、機械学習アルゴリズムの全体像をおさえておきましょう。
機械学習のアルゴリズムは、下記の図のように大きく「教師あり学習」、「教師なし学習」、「強化学習」の3種類に分かれます。
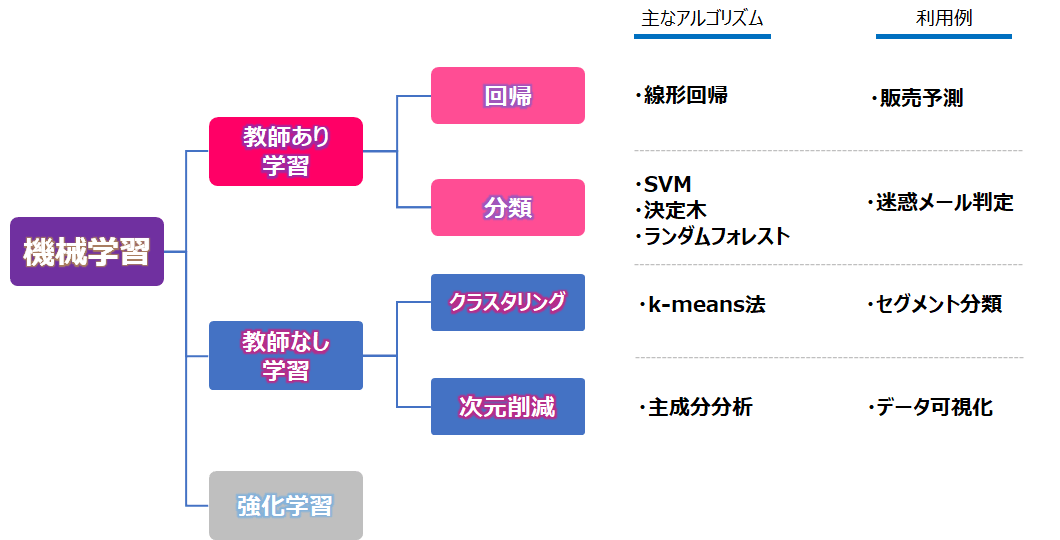
- 教師あり学習…教師データ(入力、および対応する正解ラベルの組)を用いて出力を識別・予測する手法
- 教師なし学習…教師データを使わず、データそのものの本質的な構造・特徴を明らかにする手法
- 強化学習…収益を最大化する方策を獲得することを目的とした手法
以下より、「教師あり学習」と「教師なし学習」のアルゴリズムを中心に紹介します。合わせて、pythonにおける各アルゴリズムを実装するクラスを紹介しています。
教師あり学習
教師あり学習は、教師データ(入力、および対応する正解ラベルの組)を用いて出力を識別・予測する手法です。
予測の対象によって大きく以下の2つに分類されます。
- 回帰…数値(連続値)の予測(例:過去の売上から将来売上を予測)
- 分類…カテゴリー(離散値)の予測(例:画像の犬や猫の識別)
回帰
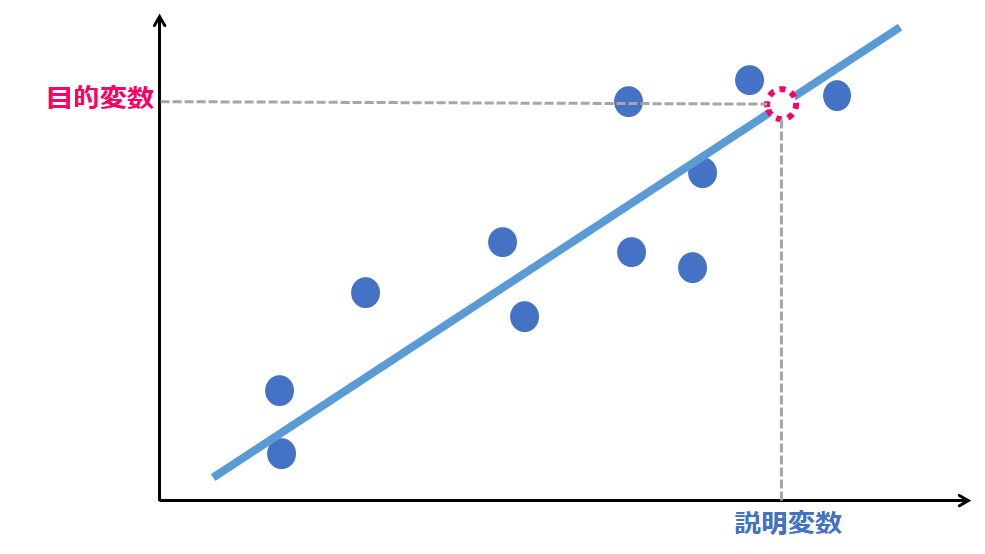
回帰は、ある値(目的変数)を単一または複数の値(説明変数、または特徴量)で予測する、教師あり学習の手法です。目的変数は予測したい変数、説明変数は予測の手がかりとなる変数です。
代表的な回帰として線形回帰が挙げられます。
線形回帰
線形回帰は統計でも用いられるスタンダードなアルゴリズムです。説明変数の数で大きく2つに分かれます。
- 単回帰分析…1つの説明変数で目的変数を予測(例:気温のみからお弁当の売上を説明)
- 重回帰分析…複数の説明変数で目的変数を予測(例:駅からの距離、築年数、物件の広さなど様々な条件から住宅家賃を説明)
y:目的変数
x:説明変数 (n=1の時は単回帰分析)
なお、線形回帰はPythonを使わずともExcelでも実現可能です。詳細は以下をご参照ください。

注意点として、重回帰分析では多重共線性(マルチコ)に留意する必要があります。多重共線性は、相関が高い特徴量の組が同時に説明変数として存在すると予測がうまくいかない現象です。
そのため重回帰分析時には特徴量をうまくとり除く必要があります(Pythonでは意識する必要はありませんが、Excelで重回帰分析を実施する際は手動で取り除かないといけません)。
分類

分類は、データのカテゴリーを予測して分ける手法です。
代表的な分類としてサポートベクターマシンや決定木、ランダムフォレストが挙げられます。
サポートベクターマシン
サポートベクターマシン(Support Vector Machine, SVN)は、マージンの最大化のもと、クラスを線形分離するアルゴリズムです。
マージンの最大化とは、下記の図のように、決定境界(クラスを分ける直線)から、クラス間のサポートベクタ(各クラスのデータ)の距離を最大にする決定境界を求める、という考え方です。
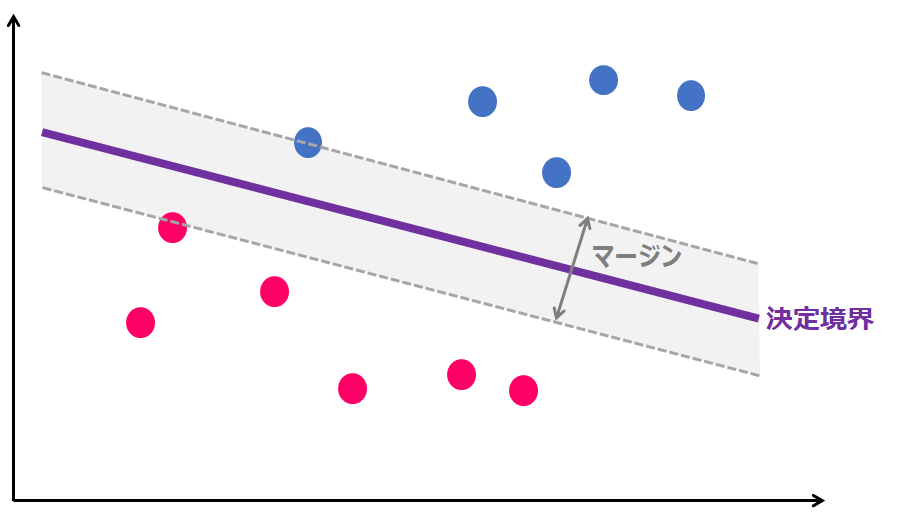
マージンが最大となる決定境界とすることで、未知のデータが誤った分類を行う可能性を最小化する汎化能力を持たせる意図があります。
決定木
決定木(Decision Tree)は、データを分割するルールを作成し、分類を複数回実行するアルゴリズムです。
決定木のポイントは、どの特徴量をどの値でデータを分割していくかです。
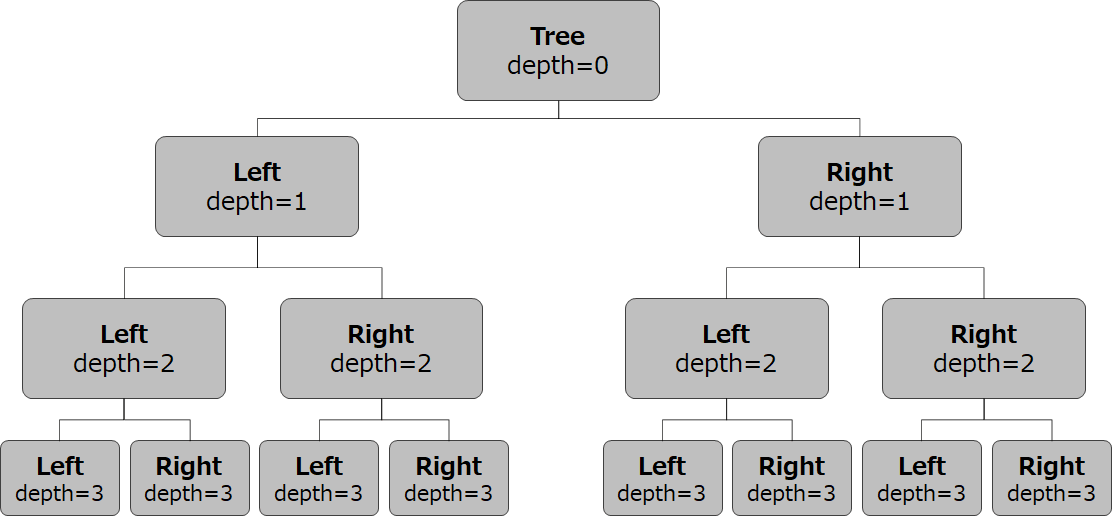
分割ルールについては機械学習の表現では、「情報利得が最も増加(不純度が最も減少)するデータ分割を行う」ですが、すなわち「データを最も綺麗に分けられる分類を行う」ということです。
ランダムフォレスト
ランダムフォレスト(Random Forest)は、データのサンプル特徴量をランダムに選択し、決定木の構築処理を複数繰り返し、各木の推定結果により分類や回帰を行うアルゴリズムです。
ランダムフォレストは決定木のアンサンブル(集合)であり、このように複数の学習器を用いた学習をアンサンブル学習と言います。
教師なし学習
教師なし学習は、教師データを使わず、データそのものの本質的な構造・特徴を明らかにする手法です。
代表的な手法は以下の2つです。
- クラスタリング…類似のデータ群を集まりに分ける(例:層別マーケティングのための顧客クラスタ化)
- 次元削減…データを失わなずに低い次元へ圧縮(例:身長と体重からBMIを算出)
クラスタリング
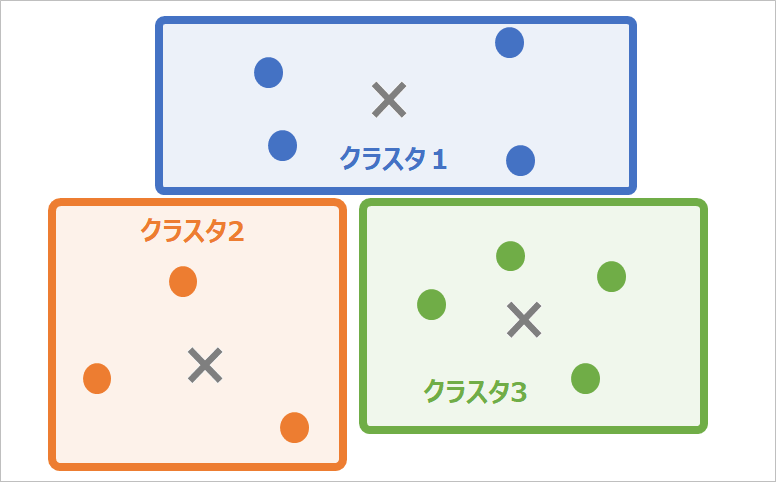
クラスタリングは、ある基準に沿ってデータ群の類似性を計算、データを集まり(クラスタ)に分ける、教師無し学習の手法です。
クラスタリングは「教師なし=クラスタが正解であることの情報がない」ため、クラスタの妥当性や、クラスタがどういったものなのか、は人が判断する必要があるのが特徴です。
注意点として、教師無し学習の「クラスタリング」と教師あり学習の「クラス分類」は異なる概念です。
- クラスタリング…データの構造から似たデータの集まりを抽出する(教師なし学習)
- クラス分類…あらかじめ設定したクラスにデータを分類する(教師あり学習)
代表的なクラスタリングとしてk-means法が挙げられます。
k-means法
k-means法は、データをk個のグループにクラスタリングするアルゴリズムです。
以下の手順でデータをクラスタリングします。
- 各データをランダムにk個のクラスタに割り当て、各クラスタの中心を重心とする
- 各データに対し最も距離が近い重心に対応するクラスタに再ラベリングする
- 重心が収束するまで繰り返す
次元削減
次元削減は、データを失わなずに低い次元へ圧縮する、教師無し学習の手法です。
代表的な次元削減として主成分分析が挙げられます。
主成分分析
主成分分析(Principal Component Analysis, PCA)は、高次元のデータを低い次元のデータに変換するアルゴリズムです。
特徴量の数が多い場合に、相関の小さい少数の特徴量(主成分)へ次元削減することに用いられます。次元削減により、学習時間を減らしたり、高次元では困難なデータの可視化ができるメリットがあります。
機械学習アルゴリズムの実装へ
ここまで機械学習の主なアルゴリズムとその特徴を紹介してきました。機械学習のアルゴリズムは多岐にわたるため、まずは全体像を整理して理解することが重要です。
アルゴリズムの概要を理解できたら、次のステップとして実際に手を動かして各アルゴリズムを実装してみましょう。Pythonの機械学習を実行するライブラリとしてscikit-learnがあります。
scikit-learnを用いて機械学習を実装すると非常に高度なデータ分析が一瞬でできることに感動、一歩も二歩も深いデータサイエンスの世界に入ることができます。
まとめ
本記事では機械学習の主なアルゴリズムとその概要を紹介してきました。
それぞれのアルゴリズムの概要が理解できていると、機械学習の肝である「解きたい課題に適切なアルゴリズムの実装」ができます。
次のステップとして、実際に手を動かして各アルゴリズムの実装をしてみてください。
また興味があれば、Python3エンジニア分析試験やG検定といった、データサイエンス系資格試験にも挑戦してはいかがでしょうか。
これらの試験については下記の記事にまとめています。ご興味あればお読みください。





コメント