「ディープラーニング(深層学習)」という言葉は、誰もが一度は聞いたことがあるものの、それが何を指しているのかすらわからない方も多いのではないでしょうか。
本記事では、ディープラーニングの正体が何か、またその構成要素や抑えるべきポイントをまとめました。
初見の用語が難しく感じられるかもしれませんが、それぞれが何を指しているかを把握していくと全体像が理解しやすいです。
ディープラーニングの正体
ディープラーニングは、ディープニューラルネットワーク(多数のニューロンを無数に繋げたニューラルネットワーク)を用いて予測・学習を行う機械学習の手法です。
1960年代にアルゴリズムが考案され、2010年代に入り脚光を浴びました。
ディープニューラルネットワークにより、複雑な関数の精度が高い予測が可能になりますが、「何に対しても万能な手法」というわけではなく(ノーフリーランチ定理)、下記のような欠点があることも理解する必要があります
- 過学習を起こしやすい
- 調整パラメータ数が多い
- 勾配消失問題が起こる
過学習:訓練誤差が小さいにも関わらず、汎化誤差が小さくならない状態
過学習を抑制するために以下のような手法が用いられます。
- LASSOなどの正則化
- ドロップアウト(重みの更新枝を一定で無効化)
勾配消失問題:誤差の勾配を逆伝播する過程で勾配が消失、入力層付近で学習ができなくなる現象
ディープニューラルネットワークの構成要素
「ディープニューラルネットワーク=多数のニューロンを無数に繋げたニューラルネットワーク」
と説明しましたが、この構造を理解するために下記の3点を理解する必要があります。
- ニューラルネットワーク…ニューロンがつながったネットワーク
- ニューロン…ニューラルネットワークの最小単位
- 活性化関数…ニューロンの入力を出力に変換する関数
ニューラルネットワーク
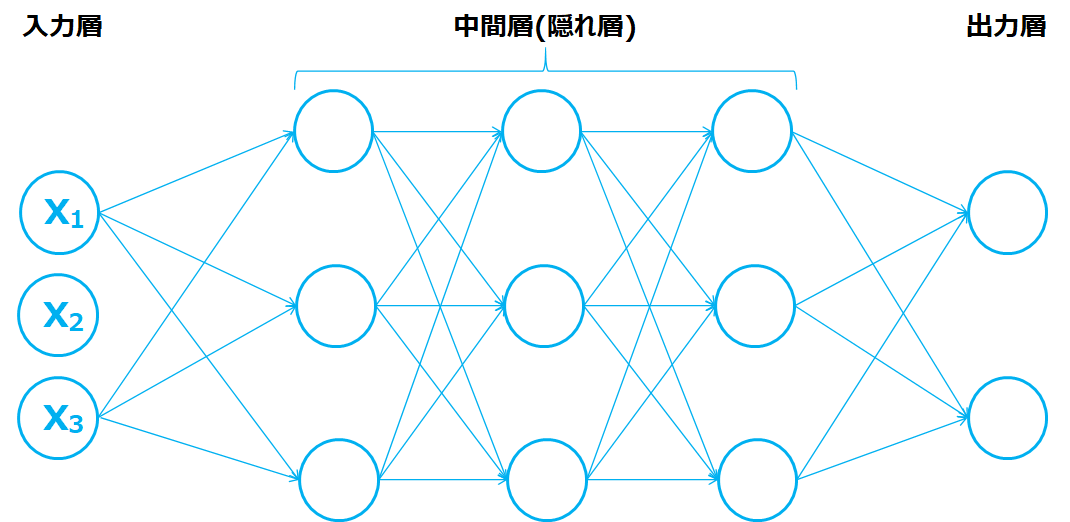
ニューラルネットワークはニューロンが多数つながれたネットワークの模式図です。
左の入力が入る層を入力層、右の出力が吐き出される層を出力層と言います。また入力層と出力層で挟まれた中間の層を中間層、または隠れ層と言います。
ニューロン
ニューロンは、ニューラルネットワークの最小単位です。
人間の脳の神経細胞を信号が伝達する様子を模倣しています。
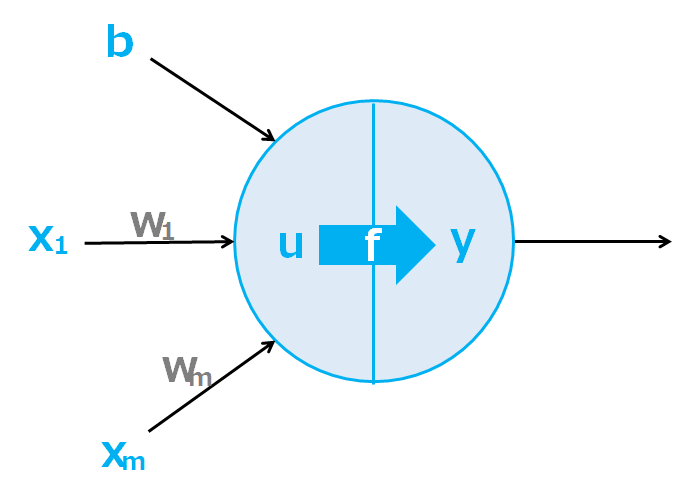
u:総入力、f:活性化関数、y=f(u) : 出力
ニューロンは入力を受け、下記の計算をすることにより予測を可能に指定します。
- 入力(x)に重み(w)が乗算され、またバイアス(b)はそのままニューロンに入る
- 入力が加算され、総入力(u)が計算(u = b + w1x1 + w2x2 + … + wmxm)
- 活性化関数(f)により出力(y=f(u))を得る
活性化関数
ニューロンの予測精度を上げるポイントは、活性化関数(f)の設定、様々な種類の関数が存在します。
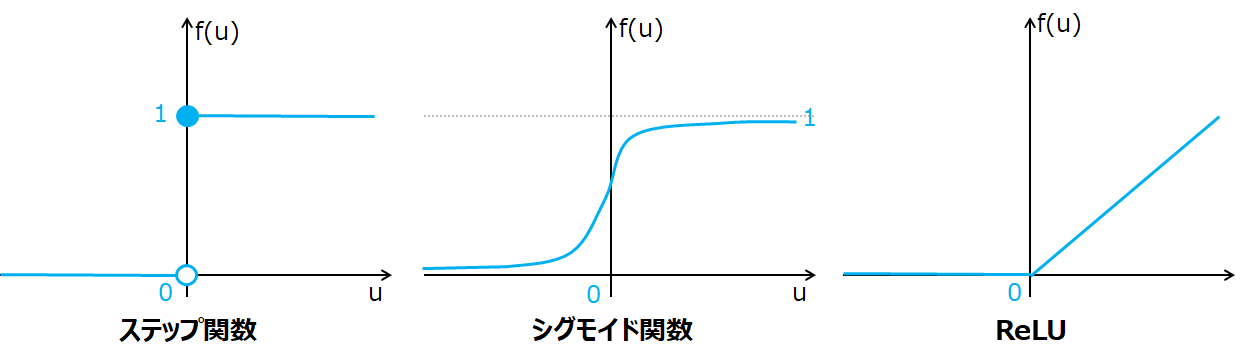
- ステップ関数…単純パーセプトロンと同じ。u=0で微分できない(接点が定まらない)ためニューラルネットワーク学習で使用できない。
- シグモイド関数…ステップ関数に類似、かつ微分ができる(接点が引ける)関数(入力を0~1の間の値に正規化する性質を持つ)。勾配消失問題が起きやすく、現在はあまり用いられていない。
- ReLU…勾配消失問題が起きにくく、形が簡単であるため現在主流。
- ソフトマックス関数…出力を確率として解釈する際に用いられる(分類問題の出力層付近で用いられる)
ステップ関数→シグモイド関数→ReLUと、そのデメリットを補う関数が用いられるようになり、現在ではReLUが主流で用いられていることがポイントです。
ディープニューラルネットワークの学習
ディープニューラルネットワークの学習においては、学習の流れをおさえるとともに、学習により異なる重みの更新タイミングや学習の注意点を理解する必要があります。
学習の流れ
ディープニューラルネットワークの学習は以下の流れで行われます。
ポイントは順伝播(左→右)で予測が行われ、逆伝播(右→左)で重みの更新が行われるサイクルとなっていることです。
- 教師データを用いて予測、予測値と正解ラベルを比較し誤差を計算(順伝播:左→右)
- 勾配降下法(重みを更新し勾配が最小になる点を探索するアルゴリズム)に基づき重みを更新、誤差を最小化(逆伝播:右→左)
- 繰り返し
重みの更新のタイミング
重みの更新タイミングは学習方法により異なります。
| 逐次学習(確率的勾配降下法) | 訓練データ1つに対し重みを更新 |
| ミニバッチ学習(ミニバッチ勾配降下法) | 訓練データの一部分に対し重みを更新 |
| バッチ学習(バッチ勾配降下法) | 訓練データすべてに対し重みを更新 |
下記の用語は意味が異なるため要注意です。上記更新により増加するのはイテレーションです。
| エポック | 訓練データを学習に用いた回数 |
| イテレーション | 重みを更新した回数 |
学習の注意点
誤差が小さくなる重みを勾配降下法で探す際、誤差を最小化する大域最適解を求めたいものの、局所最適解や停留点にトラップされる可能性に留意する必要があります。
| 大域的最適解 | 誤差を最も小さくする解 |
| 局所最適解 | 周辺では誤差の値が小さいが大域的最適解ではない解 |
| 停留点 | 大域的最適解・局所最適解ではないが勾配が0となる点 |
ディープニューラルネットワークの学習では、局所最適解を求めることを目指すのがポイントです。
勾配降下法で求められる重みでは、大域最適解か局所最適解か判断できないためです。
この問題に対処すべく考えられた手法をモーメンタム(最適化の進行方向に学習を加速させる)といいます。また、さらなる効率的な手法として現在はRMSpropやAdamが用いられています。
まとめ
ディープラーニングの基礎となる、ディープラーニングの概要についてご紹介しました。
非常に奥が深く難解なイメージがある「ディープラーニング」ですが、こういった概要を把握できると、その正体が見えてきたのではないかと思います。
ディープラーニングに少しでも興味を持たれた方は、ディープラーニングにどのような手法が使われているか、またその研究分野をまとめましたのでご参照ください。

続けて「ディープラーニング G検定 公式テキスト」を読まれてみるのもオススメです。
本書はAI・ディープラーニングの資格試験であるG検定のテキストですが、ディープラーニングの導入のための教科書でもあります。



コメント