データサイエンスの位置づけが重要となる中で必要性を増す「統計学」。
統計学を学ぶ上で、最も基礎となる考え方が「母集団」と「標本」の概念です。
これらの概念をどう扱うかによって、「記述統計」と「推測統計」2つの統計学に繋がります。
本記事では、この「母集団」と「標本」、および2つの統計学について説明します。
「母集団」と「標本」
データには「母集団」と「標本」、2つの概念があります。
例えば、テレビ番組で、以下のような報道に違和感を感じた経験はないでしょうか。
本法案については国民として『反対』の声が大きいようです。
など、様々な疑問が浮かんでいる方は、データ分析に必要な考え方ができるといえます。
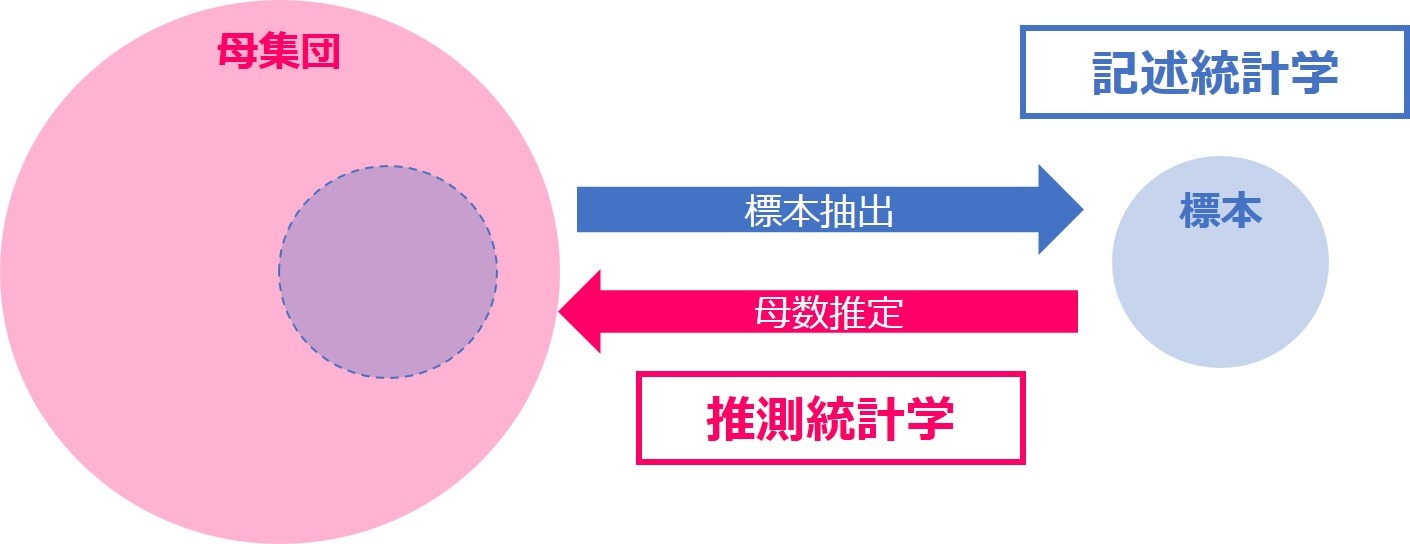
この例では、「母集団」と「標本」は以下の考え方となります。
- 母集団 …本来対象となるデータ全体(例:全国民)
- 標本 … 母集団の情報を推測するために抽出した一部のデータ(例:アンケート対象)
データ分析において、「母集団」全てのデータを知ることは稀です。
そのため、「母集団」の一部である「標本」を抽出することで、この標本の統計量を把握するすることで、母集団を推測することができます。
この流れを、それぞれ『記述統計』、『推測統計』と表現、統計学は大きくこれらの2つに分類されます。
- 記述統計 … 「標本」データを元に、データの特徴を記述(例:アンケートで70%が反対)
- 推測統計 … 「標本」から「母集団」を推測(例:国民の声は「反対」)
以下は、統計学の大きな分類であう『記述統計』および『推測統計』について詳しく説明します。
記述統計
『記述統計』とは、「標本」データが持つ情報を多面的に明確化することで、データの特性を把握することを目的とした統計です。
記述統計は、日常のあらゆる場面で登場します。
学生の試験においては「平均点」や「偏差値」の概念が良く使われますが、これらはまさに記述統計の代表格といえます。
平均点や偏差値との比較で、初めてご自身の立ち位置を把握することができます(点数は上がったが、偏差値は変わらない、など)。
記述統計を学ぶ上で最重要となる「要約統計量」について、以下に詳しく纏めていますので、ご興味あれば合わせてお読みください。

推測統計
『推測統計』は 「標本」データを元に、「母集団」や、母集団が持つ特徴を推測する統計です。
推測統計には、大きく「検定」と「推定」の考え方があります。
検定
『検定』は、ある仮説に対して、正しいか否かを統計学的に検証することにより仮説の確からしさを論証する統計手法です。
統計における『検定』のイメージがつかみづらい方も多いようですが、とても重要な概念です。
検定(統計的仮説検定)を学ぶ上で最重要となる考え方について、以下に詳しく纏めていますので、ご興味あれば合わせてお読みください。

推定
『推定』は、標本の特徴から、母集団の特性を推測する統計手法です。
データ分析における最終ゴールは、元となる母集団を、数値や範囲で具現化することです。
母数の推定には、点推定と区間推定があります。
- 点推定 : 母集団を1つの値で推定(例:母比率は65%)
- 区間推定 : 母集団を一定の幅で推定(例:母比率は60~70%)
まとめ
統計学の最も基礎の部分となる「母集団」と「標本」の考え方、およびその概念からなる「記述統計」と「推測統計」2つの統計の考え方と説明しました。
統計学をよりしっかりと理解したい方は、下記の書籍がオススメですので興味があったら一読してはいかがでしょうか。
また、さらに統計に興味を深めた方は、「統計検定」の受験をオススメします。
統計検定の記事を下記にまとめていますので、合わせてお読みください。




コメント