データサイエンスの位置づけが重要となる中で必要性を増す「統計学」ですが、統計学を学ぶ上で、重要な分析手法となるのが「多変量解析」です。
ひとことで多変量解析といっても様々な分析手法があるため苦手とする方も多いですが、それぞれの手法を理解することで、その便利さに気づくことができます。
本記事では、この「多変量解析」について説明します。
多変量解析とは
「多変量解析」は、複数の変数をまとめて統計的処理を行う手法の総称です。
下記の図のように大きく「外的基準あり」の分析、および「外的基準なし」の分析に分かれます。
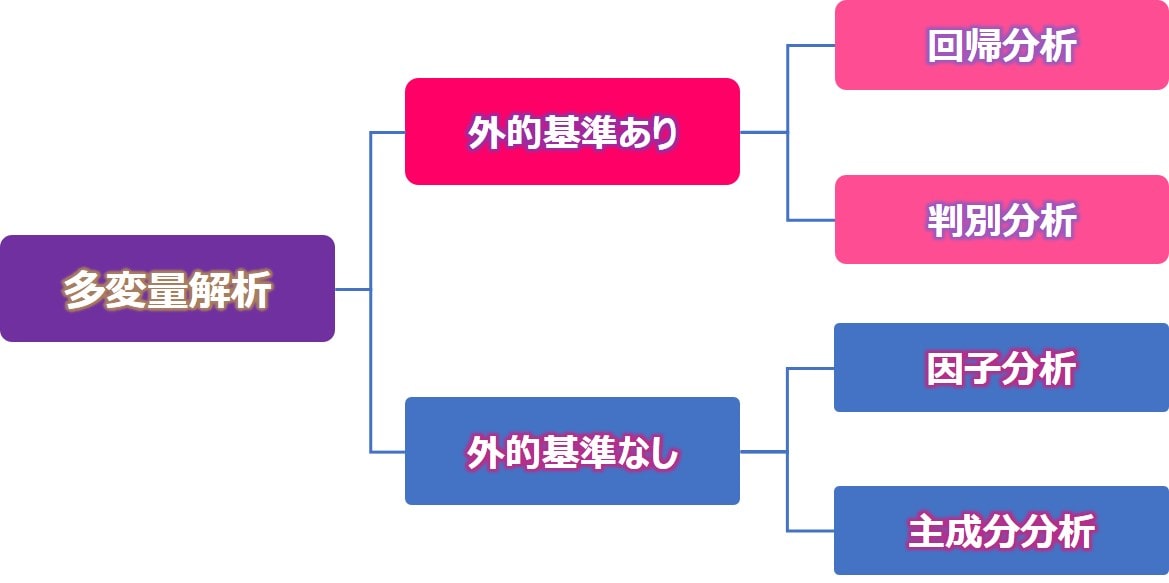
- 外的基準あり分析 … 基準を設定し、基準たる変数に対する予測・影響を解析する手法
- 外的基準なし分析 …基準を用いず、変数間の構造を解析する手法
外的基準あり分析
外的基準あり分析は、基準を設定し、基準たる変数に対する予測・影響を解析する手法です。
解析の対象によって大きく以下の2つに分類されます。
- 回帰分析…数値(連続値)の予測(例:労働時間からストレスを予測)
- 判別分析…カテゴリー(離散値)の予測(例:合格や不合格の識別)
回帰分析
回帰分析は、単一または複数の値(独立変数)からある値(従属変数)を予測する分析(従属変数は予測したい変数、独立変数は予測の手がかりとなる変数)です。
回帰分析は最も用いられる分析手法で、独立変数の数で大きく2つに分かれます。
- 単回帰分析…1つの独立変数で従属変数を予測
- 重回帰分析…複数の独立変数で従属変数を予測
y:従属変数
x:独立変数 (n=1の時は単回帰分析)
a:偏回帰係数(最小二乗法によって推定)

なお、回帰分析はExcelで行うことができます。詳細は以下をご参照ください。

注意点として、重回帰分析では多重共線性(マルチコ)に留意する必要があります。多重共線性は、相関が高い特徴量の組が同時に説明変数として存在すると予測がうまくいかない現象です。
そのため重回帰分析時には特徴量をうまくとり除く必要があります。
判別分析
判別分析は、従属変数が名義尺度(例:グループA・グループB)の場合、あるサンプルがどのグループに属するかを判別したり、逆に独立変数が判別に与える影響を分析するための手法です。

なお、独立変数が名義尺度でこれらの分析を行う場合、名義尺度をダミー変数(元の変数カテゴリーを1-0型の変数へ変換)した上で、回帰分析や判別分析を行います。
ダミー変数を用いた回帰分析を「数量化Ⅰ類」、判別分析を「数量化Ⅱ類」と言います。
外的基準なし分析
外的基準なし分析は、基準を用いず、変数間の構造を解析する手法です。
代表的な手法は以下の2つです。
- 因子分析…複数の変数間の潜在変数を抽出(例:各テスト結果の要因を記憶力と定義)
- 主成分分析…情報を集約して合成変数を作成(例:身長と体重からBMIを算出)
「因子分析」と「主成分」は混同されがちですが全くの別物ですので、比較して理解しましょう。
因子分析
因子分析は、複数の変数間に共通する潜在変数(共通因子)を抽出する分析です。

因子分析では、解が1つではなく無数にある(解の不定性)ため、分析の妥当性や、共通因子がどういったものなのか、判断する必要がある(探索的因子分析)のが特徴です。
主成分分析
主成分分析は、複数の変数の情報を集約して、合成変数(主成分)を作成する分析です。

変数の数が多い場合に、相関の小さい少数の主成分へ次元削減することで、高次元では困難なデータの可視化ができるメリットがあります。
クラスター分析
外的基準なし分析にはその他、類似するサンプルの分類を目的とする「クラスター分析」もあります。
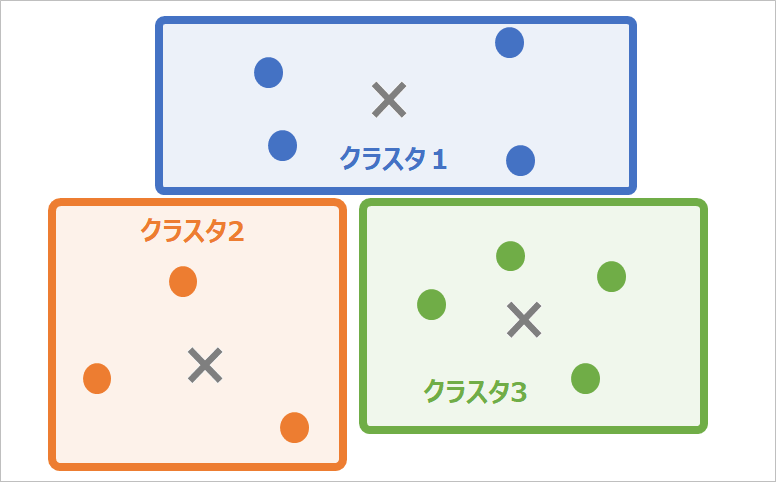
「クラスター分析」と「判別分析」は一見似ているように見えますが、全く異なる概念ですのでご注意ください。
- クラスター分析…データの構造から似たデータの集まりを抽出する(外的基準なし)
- 判別分析…あらかじめ設定したグループにデータを分類する(外的基準あり)
まとめ
統計学における重要な分析手法における「多変量解析」について説明しました。
概要について説明しましたが、この領域は一朝一夕で身に付くものではありませんので、下記の書籍などでより深い学習をオススメします。
また、実際の多変量解析は、(Excelで行える回帰分析を除くと)RやPythonなどの統計ツールやデータ解析を得意とするプログラミングを活用することでより世界が広がります。
いわゆるAIの世界における『機械学習』と言われるところでもありますので、興味がある方は、機械学習についてまとめている下記記事についても、合わせてお読みください。




コメント